From form to quantum mechanics
To come from a global picture of one form representing the universe to a quantum mechanical interpretation the following is suggested.
A local form (a simplified universe with for instance only one
particle
in it) is to be given a name, for instance electron. In FIT an
electron is a deformed (infinite) volume of space, deformed with a special kind
of symmetry. Each point in space is represented by 6 numbers. 3 for its place
in Euclidic space and 3 for its new place at a particular moment. We now make a
projection of these 6 real coordinates onto a space with 5 real coordinates.
Each point in 3D space gets assigned a number-pair (representing a complex
number). This collection of numbers gets a system name (i.e. electron) and it
represents the (probabilistic) behaviour of the system in its environment over
time. In more regular words: the particle is represented as a point-particle
with a wave function, or if you will: the subsystem is now a wave function with
a name. The projection is the process of distinguishing a system and assigning
it a wave function in space. (see for instance {Tribble} on the physicist’s use
of QM). By making the projection (seeing particles) and as such losing
information exact predictability of the behaviour of space turns into
probability of behaviour of particles.
Some comments on the measuring process:
Objects are:
the measuring system (M.S.)
the primary system (P.S.)
the measurement (M.S.- P.S. interaction)
the measuring system projection (M.S. wave function)
the primary system projection (P.S. wave function)
The global form is considered to be a superposition of two forms, the forms
of the measurement system and of the primary system. This virtual
separation between forms is done by just building the
measurement apparatus (and its ability to distinguish between certain states by
operating the apparatus). The description of the apparatus in QM consists of a
state vector and is calculated from the global form of M.S. by a projection
operator. Obviously this operator is very complex and for the time being beyond
our grasp.
At the same time the primary system is found from another projection. This projection operator reduces the global form of P.S. to the primary state vector as we know it in QM. In these two projection operators lies all our interpretation knowledge. They imply how we order space into subspaces (read i.e. particles) and their relative relations (read i.e. fields). In other words, what do we consider the system under investigation to be and what do we consider the investigating system to be.
Illustration 3: From a three dimensional cubic grid the 3D form of one sheet
(a deformed Euclidic plane) is projected on screen.
Here is a film (rotating GIF 600Kb) that
shows how a flat wave
is bouncing against a wall (blue line)
with two slits in it.
The continuing interference pattern
becomes visible and also the effect of a pseudo black hole
behind the wall. In the film different
slit-distances are made visible. The two red lines are
visualising two screens at different distances from
the wall as in the classic two slit experiment.
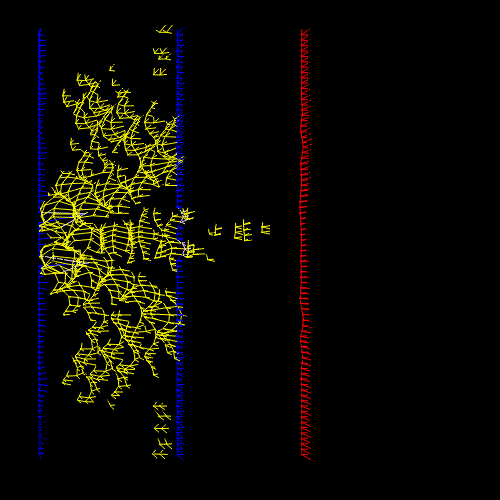
Illustration 4: Here is an impression (rotating GIF 1.5Mb) of a projection of space. Only those places in space with enough deformation are coloured yellow. The space between the two blue lines can be interpreted as a cavity with 4 holes in it. The holes in the left blue line generate energy. The two holes in the right blue line emit energy. Sort of an impression of particles existing for a brief period ("quantum foam") and interacting with a screen, creating an interference pattern.
From form to relativity theory
To come from one form representing the universe to the interpretation of relativity theory we can imagine the following.
Complex subforms
like stars, consisting of subforms
called
particles represent masses in space. The space in between the particles is
deformed or stretched and waving
just as it is in FIT and influences
the movement of the subforms. In fact it is one and the same form but once you
start classifying, once you make distinctions and subdivide, you have to start
giving names to the different objects (and their attributes such as mass) and
their relations (forces or stretched space).
When going from a global picture to a local picture with different objects and their relations it also becomes necessary to introduce a second type of time to measure relative change in space. This is the kind of time we are familiar with and we use in relativity theory. The global time is visible in what we call the speed of light. Space deformations like photons travel with a speed that directly relates to the stiffness of space.
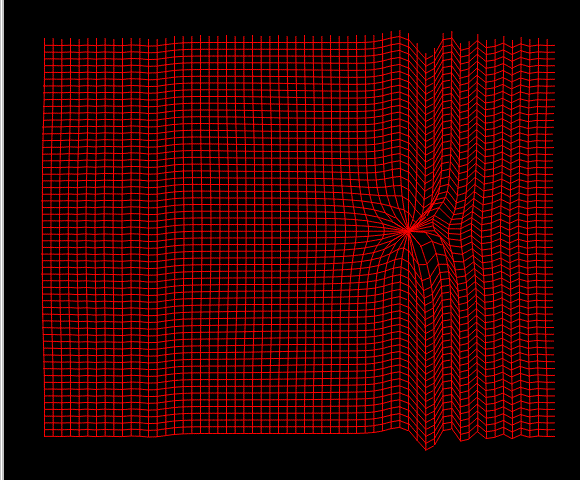
Illustration 5: From a three dimensional cubic grid the 3D form of one sheet
(a deformed Euclidic plane) is projected on screen.
Here is a film (rotating GIF 1.9Mb) that
shows how a pseudo flat gravitation wave
encounters a pseudo black
hole
.
From form to string theory
To me it is very informative to create these (discretised elastic 3D) spaces
in the computer. To create a deformation one can take a point or a line of
points or a two dimensional membrane of points or a volume of points and start
moving and distorting it in space. This will obviously influence all the rest
of space. Coupling FIT to string theory would in my opinion be established by
finding the right strings
that manipulate
their surroundings so
the environment looks like a particle we know and recognize from the behaviour
we can measure with our measuring devices. In a way we go from a global 3 x 3
matrix (that represents the new form of space) to a local 3 x 3 matrix to
describe a particle. Again we go from a global picture of one-ness
to a
discrete picture in which we see strings that interact.
From form to loop-quantum-gravity (LQG)
For me it would be very interesting to hear what loop-quantum-gravity physicists, who would momentarily adopt FIT for the sake of argument, would say if they tried to compare the concepts of LQG to the assumptions of FIT. I would not be surprised if FIT could shed light and suggest modifications on some of the assumptions that still cause difficulties in LQG. Specifically the result that space may be discretised seems to me to be a snake biting its own tail resulting from the discretised world of quantum mechanics. Combining GR and QM without an intermediate, I would imagine, has to have the result of either a discretised space (knot states as quanta of space if you fit GR to QM) or a disappearance of the particle view (if you fit QM to GR in a theory that would maybe be called gravitational quantum mechanics). Furthermore I suspect that in a discretised space, the law of conservation of energy will slightly fluctuate and will only hold in the limit where discrete becomes continuous. I would be very interested to hear if any of such calculations exist. In my own grid, which by its very nature is discrete, what I consider to be the analog of energy is stabel but fluctuates just a bit. Fluctuations depend on the relative deformation of the grid. Only locally infinitely small deformations result in zero fluctuation. I need a continuum to uphold the law of energy conservation on all scales (which for some reason I would prefer from an aesthetic point of view).
The speed of light and Planck’s constant
Let's assume the assumptions are right and its a given that there is only
space, that we are made of distorted space
. Then we should be able to
explain where the most important constants, that we know in physics, come from.
My suspicions:
The speed of light can be deduced from the relation between the deformation of space and its
willingness
to return to uniformity, (like excess pressure related to excess density for deducing the speed of sound) involving the elasticity and stiffness of the medium called space. In reality it will be the other way around and we will deduce the stiffness of space from the speed of light.Planck's constant and the whole concept of quantisation may be derived from the stiffness of space putting a maximum on the deformability per unit length of space. This maximum deformability will result in a minimal distance between two points that can be folded
onto each other
and as such this minimal distance will be the deciding factor in thediscretisation
of space, the construction of length scales in the symmetries in particle-deformations and Planck's constant.